I’ve always loved mathematics and geometry. One of my favorite concepts is tessellation. A tessellation is a geometric pattern of polygons fitted together to cover an entire plane without overlapping or having any space between the edges.

A very simple idea of tessellation is an arrangement of squares in a checkered board or a mosaic tile pattern.

The word “tessellate” is derived from the Ionic version of the Greek word “tesseres” which translates to mean “four”. This is because the first tessellations were made using four sided figures most commonly the square, or rectangles.

A Regular Tessellation is one in which all of the polygons are congruent and regular, with common vertices. The mathematician Kepler (1571-1630) investigated the possibility of filling the plane with regular polygons. Only three regular polygons can be tessellated in the Euclidean plane: the equilateral triangle, the square, and the regular hexagon.

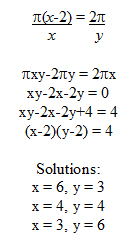
Let x be the number of sides for each polygon and y the number of polygons coming together at each vertex. Then the two expressions for the measure of each angle at a vertex can be set equal.

This means that only a 6, 4 and 3 sided figure meeting at 3, 4, and 6 vertices can be tiled to completely fill the Euclidean Plane.

POLYGON ANGLE DEGREES

Another way to prove it, for a polygon to completely fill the plane, each interior angle must be a divisor of 360º. Each angle of a regular triangle is 60º, a square is 90º, and a hexagon has angles measuring 120º all of which you can see divide perfectly into 360º. All other regular polygon do not have angles equally divisible by 360º

What shapes can form Tessellations?
Any 3 or 4 sided shape.

When considering non-regular polygons in the Euclidean plane, possibilities for tessellation become endless. Any three or four sided figure can be tessellated. When discussing these types of tessellations we must consider the movement of the polygons within the plane to allow for their tessellation. Figures can be moved using either rotation, translation, reflection, or glide reflection.

Rotation is movement by a certain angle around a center point. Translation is moving an object a certain distance without rotating, or reflecting it. Reflection is creating an object’s mirror image in respect to a line, and glide reflection combines a reflection with a translation along the direction of the mirror line. The movement of the polygons will not effect their angles, sizes, and shapes.
Tessellated Architecture Examples

Great Court of the British Museum One of the best examples of tessellation in architecture is the roof of the British Museum made of glass triangles. The Great Court tessellated roof was designed by London-based architects Foster + Partners. You can visit the British Museum official website if you are in the area and want to see it in person. The Museum has free admission.

Tile floors, patios and bricks are also other examples of tessellations that you may find in architecture.

Tessellations are all around you and used in many common places in the world.